Profinite group

In mathematics, profinite groups are topological groups that are in a certain sense assembled from finite groups; they share many properties with their finite quotients.

Contents 1 Definition 2 Examples 3 Properties and facts 4 Profinite completion 5 Ind-finite groups 6 See also 7 References

Definition

Formally, a profinite group is a Hausdorff, compact, and totally disconnected topological group: that is, a topological group that is also a Stone space. Equivalently, one can define a profinite group to be a topological group that is isomorphic to the inverse limit of an inverse system of discrete finite groups. In categorical terms, this is a special case of a (co)filtered limit construction.

Examples

• Finite groups are profinite, if given the discrete topology.

• The group of p-adic integers Z_p under addition is profinite (in fact procyclic). It is the inverse limit of the finite groups Z/pⁿZ where n ranges over all natural numbers and the natural maps Z/pⁿZ → Z/p^mZ (n≥m) are used for the limit process. The topology on this profinite group is the same as the topology arising from the p-adic valuation on Z_p.

• The Galois theory of field extensions of infinite degree gives rise naturally to Galois groups that are profinite. Specifically, if L/K is a Galois extension, we consider the group G = Gal(L/K) consisting of all field automorphisms of L which keep all elements of K fixed. This group is the inverse limit of the finite groups Gal(F/K), where F ranges over all intermediate fields such that F/K is a finite Galois extension. For the limit process, we use the restriction homomorphisms Gal(F₁/K) → Gal(F₂/K), where F₂ ⊆ F₁. The topology we obtain on Gal(L/K) is known as the Krull topology after Wolfgang Krull. Waterhouse showed that every profinite group is isomorphic to one arising from the Galois theory of some field K; but one cannot (yet) control which field K will be in this case. In fact, for many fields K one does not know in general precisely which finite groups occur as Galois groups over K. This is the inverse Galois problem for a field K. (For some fields K the inverse Galois problem is settled, such as the field of rational functions in one variable over the complex numbers.)

• The fundamental groups considered in algebraic geometry are also profinite groups, roughly speaking because the algebra can only 'see' finite coverings of an algebraic variety. The fundamental groups of algebraic topology, however, are in general not profinite.

Properties and facts

• Every product of (arbitrarily many) profinite groups is profinite; the topology arising from the profiniteness agrees with the product topology. The inverse limit of an inverse system of profinite groups with continuous transition maps is profinite and the inverse limit functor is exact on the category of profinite groups. Further, being profinite is an extension property.

• Every closed subgroup of a profinite group is itself profinite; the topology arising from the profiniteness agrees with the subspace topology. If N is a closed normal subgroup of a profinite group G, then the factor group G/N is profinite; the topology arising from the profiniteness agrees with the quotient topology.
• Since every profinite group G is compact Hausdorff, we have a Haar measure on G, which allows us to measure the "size" of subsets of G, compute certain probabilities, and integrate functions on G.
• A subgroup of a profinite group is open if and only if it is closed and has finite index.
• According to a theorem of Nikolay Nikolov and Dan Segal, in any topologically finitely-generated profinite group (that is, a profinite group that has a dense finitely-generated subgroup) the subgroups of finite index are open. This generalizes an earlier analogous result of Jean-Pierre Serre for topologically finitely-generated pro-p groups. The proof uses the classification of finite simple groups.
• As an easy corollary of the Nikolov-Segal result above, any surjective discrete group homomorphism φ: G → H between profinite groups G and H is continuous as long as G is topologically finitely-generated. Indeed, any open subgroup of H is of finite index, so its preimage in G is also of finite index, hence it must be open.
• Suppose G and H are topologically finitely-generated profinite groups which are isomorphic as discrete groups by an isomorphism ι. Then ι is bijective and continuous by the above result. Furthermore, ι⁻¹ is also continuous, so ι is a homeomorphism. Therefore the topology on a topologically finitely-generated profinite group is uniquely determined by its algebraic structure.

Profinite completion

Given an arbitrary group G, there is a related profinite group G^{^}, the profinite completion of G. It is defined as the inverse limit of the groups G/N, where N runs through the normal subgroups in G of finite index (these normal subgroups are partially ordered by inclusion, which translates into an inverse system of natural homomorphisms between the quotients). There is a natural homomorphism η : G → G^{^}, and the image of G under this homomorphism is dense in G^{^}. The homomorphism η is injective if and only if the group G is residually finite (i.e., 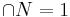, where the intersection runs through all normal subgroups of finite index). The homomorphism η is characterized by the following universal property: given any profinite group H and any group homomorphism f : G → H, there exists a unique continuous group homomorphism g : G^{^} → H with f = gη.

Ind-finite groups

There is a notion of ind-finite group, which is the concept dual to profinite groups; i.e. a group G is ind-finite if it is the direct limit of an inductive system of finite groups. The usual terminology is different: a group G is called locally finite if every finitely-generated subgroup is finite. This is equivalent, in fact, to being 'ind-finite'.

By applying Pontryagin duality, one can see that abelian profinite groups are in duality with locally finite discrete abelian groups. The latter are just the abelian torsion groups.

See also

• Locally cyclic group
• Pro-p group
• Residual property (mathematics)

References

• Nikolov, Nikolay; Segal, Dan (2006). "On finitely generated profinite groups. I. strong completeness and uniform bounds". arXiv:math.GR/0604399 [math.GR]. .
• Nikolov, Nikolay; Segal, Dan (2006). "On finitely generated profinite groups. II. products in quasisimple groups". arXiv:math.GR/0604400 [math.GR]. .
• Lenstra, Hendrik (2003), Profinite Groups, talk given at Oberwolfach, http://websites.math.leidenuniv.nl/algebra/Lenstra-Profinite.pdf .
• Lubotzky, Alexander (2001), "Book Review", Bulletin of the American Mathematical Society 38 (4): 475–479, doi:10.1090/S0273-0979-01-00914-4 . Review of several books about profinite groups.
• Serre, Jean-Pierre (1994), Cohomologie galoisienne, Lecture Notes in Mathematics, 5, Springer-Verlag, ISBN 978-3-540-58002-7, MR1324577 .
• Waterhouse, William C. (1973), "Profinite groups are Galois groups", Proceedings of the American Mathematical Society (Proceedings of the American Mathematical Society, Vol. 42, No. 2) 42 (2): 639–640, doi:10.2307/2039560, JSTOR 2039560 .